Evaluation of risk factors in patients with breast cancer in stages III and IV: comparison of Cox and Fine-Grey competing risk regression models

Abstract

Introduction: The aim of this study is to fit Fine-Grey competing risk model and compare its results with stratified Cox model and to examine its application in breast cancer data.

Methods: The study was conducted on 15830 women diagnosed with breast cancer in British Columbia, Canada. They were divided into four groups according to patients' stage of disease then for patients with stage III and IV breast cancer was fitted Cox's model and Fine-Grey competing risk flexible models to each group.

Results: The data show that Out of 1888 patients, 578 lied in the age group of below 50 years old, while 1310 were above 50 years of age. The results obtained from fitting stratified Cox regression model indicate that the variables of age and surgery are significant. The patients in the age group of below 50 years old have 70% less hazard in comparison with people older than 50 years of age (HR=0.83). Further, the patients receiving surgery have 38% less hazard in comparison with the patients not receiving surgery (HR=0.62). Then we fit Fine-Grey competing risk models. the variable of chemotherapy is significant in both parametric and semi-parametric competing risk models, and its hazard ratio is HR=1.15 and HR=1.14 in the two models, respectively. On the other hand, the variable of age has not become significant in any of the models, and its hazard ratio is HR=0.92 and HR=0.93, respectively. The variable of surgery in the competing risk parametric model is significant with an HR of 0.67. In Cox model, the variable of surgery is also significant with HR=0.62. Moreover, the variable of age in the competing risk parametric model has not become significant (HR=0.92), and in contrast the variable of age in the Cox model is significant (HR=0.83).

Conclusion: The results of this study show that Considering the comparison of the two models, it is observed that regardless of the properties of competing risk data, estimations of hazard ratio and the extent of significance resulting from Cox models are different from those of competing risk models. 

Introduction

According to the literature, breast cancer is the most common type of cancer among women. In the world, following lung and stomach cancers, breast cancer is the third most common cancer. It rarely occurs in men. Of about every 9 women, one will be afflicted by breast cancer throughout her lifetime Azizi et al., 2000. Epidemiological studies have specified many risk factors associated with breast cancer. In spite of the large number of the risk factors, only a limited number of them are highly associated with development of breast cancer, and no single cause or combination of causes can predict incidence of breast cancer in a specific person Azizi et al., 2000. For treatment of this cancer, given the stage of the cancer and medical history of the patient, breast surgery, radiotherapy, chemotherapy, or hormone therapy might be required. In most cases, two or more therapeutic methods are used simultaneously Azizi et al., 2000.

In survival data especially in medical research, sometimes every person can experience more than one type of incidence (or risk), and occurrence of one of them prevents occurrence of the others. This state is called competing risk Gichangi and Vach, 2005. One example of competing risk data in cancer data includes relapse of disease and death caused by cancer Scheike and Zhang, 2008. When a person experiences an incidence instead of the intended incidence, the probability of the incidence will change. Therefore, competing risk analysis should be performed Pintilie, 2006. The status of competing risks is not similar to censorship; in the latter the probability of occurrence of the intended incidence will be positive in the future. On the other hand, in the competing risk, occurrence of an incidence prevents occurrence of other incidents Scheike and Zhang, 2008.

One of the widely used functions in analyzing competing risk data is cumulative incidence function. There are various methods for estimating and evaluating the effect of auxiliary variables in competing risk data through the cumulative incidence function modeling. In the standard methods for modeling cumulative incidence function, first the regression model is fitted for all cause-specific hazard functions. Thereafter, the modeling of the cumulative incidence function is performed as a function of all cause-specific hazards for a set of auxiliary variables. Therefore, the cumulative incidence function is modeled indirectly and through cause-specific hazards. On the other hand, in direct modeling, regardless of modeling cause-specific hazards, the cumulative incidence function is modeled directly. In this modeling, the effect of auxiliary variables on the cumulative incidence function can be evaluated directly and the time-dependent auxiliary variables can also be examined. The outcome resulting from auxiliary variables using typical survival analysis methods will be different from the output of competing risk models. In the current methods available, it is not possible to investigate time-dependent auxiliary variables on cumulative incidence function. Most often, the effect of auxiliary variables on the cumulative incidence function is modeled through the model of proportional hazards for a cause-specific function, where the assumption of proportionality of the hazards Cox and Oakes, 1984 is very limiting and might not hold true.

Materials-Methods

The studies conducted so far on modeling competing risk data are mostly standard methods that are used for survival analysis. One of these methods is stratified Cox regression. Cox proportional hazard model or Cox regression is a semi-parametric method which not only estimates survival probabilities at different times but also investigates the effect of auxiliary variables as well. This model is defined as follows:

h(t|X)=h0(t)exp(βx)

t represents the rate of hazard over time, h (t|x), in which the basic hazard rate is h0(t) and X is for an individual with auxiliary variables. To fit the Cox model to the data, the proportional hazard assumption should hold true. This means that the ratio of hazard in the two groups should be constant over time. If the proportional hazard assumption does not hold true, stratified Cox model or generalized Cox model should be used Baghestani, 2014. In this model, estimation and interpretation of the results are simple, leading to greater applications. The most important disadvantage regarding Cox model in competing risk data analysis is censorship of competing risks Pintilie, 2006. The competing risk model predicts hazards for an intended incidence by considering other risks.

In this research, Cox model with the auxiliary variables present in this data set is as follows:

h(t|z) = ho(t)exp(β1age + β2 Stage + β3 Surgery + β4radiotherapy + β5chemotherapy

To find estimation of the effect by the Cox proportional hazards model, Schoenfeld residuals should first be used to examine whether the proportional hazards (PH) assumption holds true for each of the variables. If these assumptions are not in place for the variables, data fitting is performed by stratified Cox model.

Fine-Grey competing risk flexible models

Cause-specific hazards modeling offers a complex nonlinear modeled relationship for cumulative incidence curves. Therefore, investigation of the effect of auxiliary variables and identifying the time-dependent effects will be difficult. Recently, direct modeling of cumulative incidence function has been proposed.

The Fine and Grey modeled hazard function and Cox model are shown as the following equations, respectively:

λ_k^*(t;x)=-dlog{1-p_k(t;x)}/dt

λ₁^*(t;x)=λ₁₀exp{β^Tx}

Based on the above, they state direct modeling of cumulative incidence function as below:

P₁(t;x)=1-exp{-Λ₁(t)exp(x^Tβ)},

Where, Ʌ(t) is the unknown incremental function and β is a vector of regression coefficients. Fine-Grey competing risk parametric model does not include time-dependent variables.

Therefore, we investigated a class of competing risk flexible models as the following form, where the parametric and nonparametric model of Fine-Grey competing risk is a special state of that. We have:

h {P1(t; x, z)} = x η(t)^T + g(γ, z, t)

Where, h is the specific bond function and g is a known regression function. η(t) and represent unknown function and regression parameter, respectively.

In this research, we investigated two groups of flexible models, multiplicative models, cloglog{1 - P₁(t;x;z)} = η(t)^Tx + γ^Tz and summative models, -log{1 - P₁(t;x;z)} = η(t)^Tx + (γ^Tz)t,

Here, x is the auxiliary variable of the next P+1 (x=(1,x1,…xp)), and Z represents the auxiliary variable of the next q. In these flexible models, x has a time-dependent effect, while z has a time constant effect Scheike and Zhang, 2008. The function and regression coefficient η(t) and , respectively, are estimated by direct binomial regression method.

To fit the competing risk model, first we fit the nonparametric multiplicative model of Fine-Grey competing risk. The variables of age, stage of disease, and treatments are introduced into the model. Using nonparametric effects test, we investigated the significance of each of the time-dependent variables. Thereafter, using “Cramér–von Mises” test, we investigated the time dependency effect of each variable.

The aim of this study was to fit Fine-Grey competing risk model and compare its results with stratified Cox model and to examine its application in breast cancer data.

Results

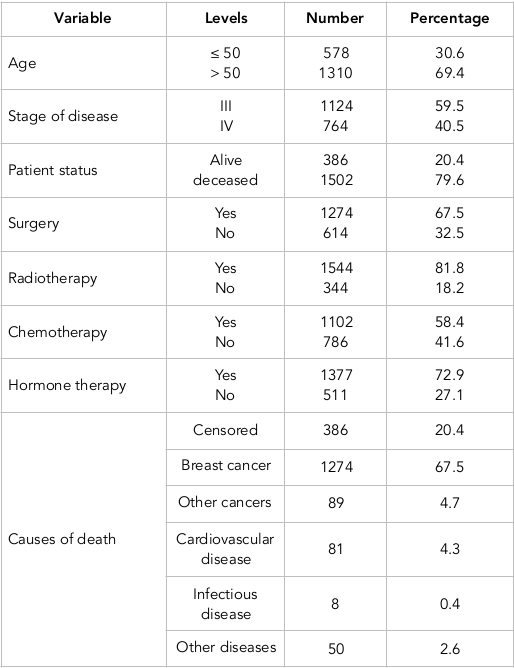
Out of 1888 patients, 578 were in the age group of below 50 years old, while 1310 were above 50 years of age. The mean and standard deviation of the age of 50(-) patients were 42.8 and 5.7 years, respectively, and their corresponding values of survival time were 7.2 and 6.02 years, respectively. On the other hand, the mean and standard deviation of the age of 50(+) patients were 67.2 and 10.1, respectively, with corresponding survival times of 5.1 and 5.04 years, respectively. The causes of death were categorized into five general groups including death resulting from breast cancer, other cancers, cardiovascular disease, infective disease, and other diseases. Due to the low number of frequencies, we finally categorized the causes of death into two groups: death resulting from breast cancer and death caused by other causes. The risk of interest in this study was considered death caused by breast cancer, while other causes were considered as the competing risk. A total of 1,274 patients had experienced incidence of death due to breast cancer, while 228 patients had experienced incidence of death due to other causes. Eventually, 386 had remained alive (i.e. they had the censorship status). Table 1 provides the frequency distribution of some factors in patients suffering from breast cancer for the entire data and the data associated with the model fitting; we first fit the Cox model.

Download figure
Enlarge figure

Table 1.

Based on the results obtained from fitting the Cox regression model and the insignificance of combination of treatments together and with other auxiliary variables, only four major combinations of treatments, age, and stage of the disease were introduced into the model Saadat, 2010. The assumption of proportional hazards (PH) was examined by Schoenfeld residuals for each variable. The PH assumption did not hold true for the variables of stage of disease, radiotherapy, chemotherapy, and hormone therapy. Thus, we fit stratified Cox model with the variables of age and surgery instead of Cox PH model.

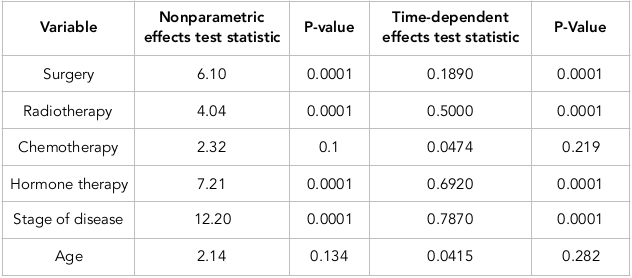
The results obtained from fitting stratified Cox regression model indicate that the variables of age and surgery are significant. The patients in the age group of below 50 years old have 70% less hazard in comparison with people older than 50 years of age (HR=0.83). Furthermore, the patients receiving surgery have 38% less hazard in comparison with the patients not receiving surgery (HR=0.62). We fit the Fine-Grey competing risk nonparametric multiplicative model. We introduced the variables of age, stage of disease, and treatments into the model. Thereafter, using “Cramér–von Mises” test, we investigated the time dependency effect of each variable.

According to Table 2 , the results of the test indicated that the variables of surgery, radiotherapy, hormone therapy, and stage of disease have become significant, while the variables of chemotherapy and age were shown to be insignificant. These two latter variables have time constancy effect, whereas the variables of surgery, radiotherapy, hormone therapy, and stage of disease have time-dependent effects. According to the results of the Fine-Grey competing risk nonparametric multiplicative model and the Fine-Grey semi parametric multiplicative model, and regardless of the time dependency of some variables, we fit the Fine-Grey parametric multiplicative model and compared its results with each other.

Download figure
Enlarge figure

Table 2.

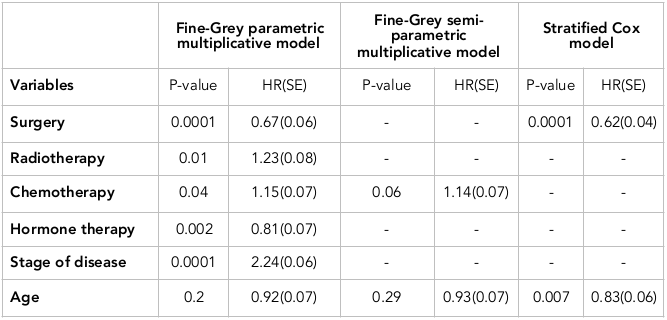
According to Table 3 , the variable of chemotherapy was significant in both parametric and semi-parametric competing risk models, and its hazard ratio was HR=1.15 and HR=1.14 in the two models, respectively. On the other hand, the variable of age was not significant in any of the models, and its hazard ratio was HR=0.92 and HR=0.93, respectively.

Download figure
Enlarge figure

Table 3.

The variable of surgery in the competing risk parametric model was significant with an HR of 0.67. In Cox model, the variable of surgery was also significant with HR=0.62. Moreover, the variable of age in the competing risk parametric model was not significant (HR=0.92), and in contrast, the variable of age in the Cox model was significant (HR=0.83).

Discussion

In the study by Nottage et al. in 2006 on breast cancer patients and using Cox model, it was found that the HR for the patients below 40 years old in comparison with those above 40 years was HR=0.79, which was almost significant Nottage et al., 2006. In the study by Zhou et al. (2011) on breast cancer patients and using stratified Cox model, it was observed that HR was 0.96 for patients above 65 years old in comparison with those below 65, which was not significant (Zhou et al., 2011). In research by Zhang et al. (2008) on breast cancer patients and using competing risk model, HR=0.71 was obtained for the variable of age, which was significant Scheike and Zhang, 2008. Moreover, in the study by Chapman et al. (2008) on breast cancer patients and using Cox model, it was seen that for patients below 70 years old, in comparison with those above 70, HR was 0.98, which was significant. HR=0.97 was obtained for the patients receiving chemotherapy, which was not significant Chapman et al., 2008. In the study by Robson et al. (2004) on breast cancer patients and using Cox model, it was found that HR was 0.55 for the patients above 50 years old in comparison with those below 50, which was significant. HR=4.8 was obtained for the patients receiving chemotherapy which was significant Robson et al., 2004. In the study by Klein in 2006, on breast cancer patients and using Cox model, it was found that HR was 1.59, which was significant for the patients above 40 years old in comparison with those below 40 Klein, 2006. Furthermore, in the study by Wolbers et al. (2009) on cardiovascular patients, Cox and competing risk model was fitted in the presence of competing risks. Neglecting competing risks and by censoring them, Cox model estimated the intended HR more than that of the competing risk model Wolbers et al., 2009.

The research by Lim on diabetic patients as well as Latouche et al. on blood cancer patients indicated that HR is different in Cox and competing risk models Latouche and Porcher, 2007Lim et al., 2010. The study by Tai et al. indicated that for analyzing competitive risk data, unlike competing risk model, Cox model overestimates HR ratios Tai et al., 2011. Comparing cause-specific hazard model and competing risk model, Tai et al. found that without considering competing risks, analysis of the effect of different treatments results in different outcomes Tai et al., 2010. Taghipour et al. (2012) showed in breast cancer patients that using Cox model in analyzing competitive risk data, HR was 1.1, which was significant for the patients above 50 years old, in comparison with those below 50 (p<0.0001) Taghipour et al., 2012.

In the study by McPherson et al. (2000), in breast cancer patients, using Cox model in analyzing competitive risk data, the risk of death was found to increase with age McPherson k, 2000. He et al. (2011), in competing risk model, showed that the HR of those older than 65 years of age in comparison with patients below 65 was 1.56 (p=0.26); in Cox model, the corresponding hazard was equal to 1.39 (p=0.01) (He et al., 2011). Similarly, Patnaik et al. (2011) analyzed competing risk data and employed Cox model, and showed that the hazard of mortality among women increases with age Patnaik et al., 2011. Arriagadal et al. (1992) also analyzed competitive risk data and found that estimations based on the competing risk model are unbiased Arriagada et al., 1992.

Based on another model, except for competing risk, the data are overestimated like Kaplan-Meyer. In the study by Pfeiffer (2013), analyzing competing risk data, by employing Cox model, the hazard of women above 50 years old in comparison with those below 50 was estimated as 1.54 Pfeiffer et al., 2013. For this reason, we fitted Fine-Grey competing risk models with multiplicative bond function, and then compared its results with stratified Cox model. Indeed, improper usage of models including Cox or Alene in competing risk data will lead to different results.

In the study by Wolbers et al. (2009) in competing risk data, the research was performed on 4,144 cardiovascular patients Wolbers et al., 2009. Cox and Fine-Grey competing risk multiplicative parametric models were fitted. The results indicated that the estimated HR was different between the two models Wolbers et al., 2009. Further, in the research by Guiterz et al. (2009), in competing risk data on 324 men with HIV infection, it was found that the variables did not become significant in both models, and the HR obtained from the Fine-Grey competing risk multiplicative parametric model was different from that of the Cox model Gutierrez, 2009. Guiterz et al. (2010), in competing risk data on 423 patients with breast cancer, observed that the hazard ratio was different for the Cox and Fine-Grey competing risk multiplicative parametric models, and the variables did not become significant in the Cox model, whereas they were significant in Fine-Grey model Gutierrez, 2010. Berry et al. (2010), in competing risk data of a joint disease, observed that the difference of the estimations resulting from Cox and Fine-Grey multiplicative parametric models was very large for HR Berry et al., 2010. Lastly, Varhan et al. (2010), in competing risk data associated with 483 patients with prostate cancer and results obtained from fitting Fine-Grey competing risk multiplicative parametric model and Cox model, observed that the HR for the variable of treatment was different in the two models and that in both models, this variable was not significant Varadhan et al., 2010.

Conclusion

Considering the comparison of the two models, we observed that regardless of the properties of competing risk data, the estimations of hazard ratio and extent of significance resulting from Cox models are different from those of competing risk models. In competing risks data, using common methods of analyzing survival data, ignoring the risks of competition leads to different results of Fine-Grey competing risks models. In the standard method, one cannot consider time-dependent covariates on the cumulative incidence function. Often, the effect of covariates on the cumulative incidence function is modeling to the cause-specific model through proportional hazard model and that proportional assumption is very limited in practice and may not hold. When proportional hazard assumption is not permitted, cannot use the standard methods for modeling the cumulative incidence function.

Author Contribution

Monireh Dehghani Arani conceived of the study, and participated in its design and statistical analysis. Yousef Bashiri conceived of the study, and participated in its design, coordination, revised the manuscript. Alireza Abadi, Parvin Yavari and, Liley Mahmudi performed the statistical analysis and drafted the manuscript. CB participated in coordination and in its design and revision of the manuscript. All authors read and approve the final version of manuscript.